Canonical low-rank approximations for uncertainty propagation, reliability and sensitivity analysis
Principal investigator: Katerina Konakli
Description
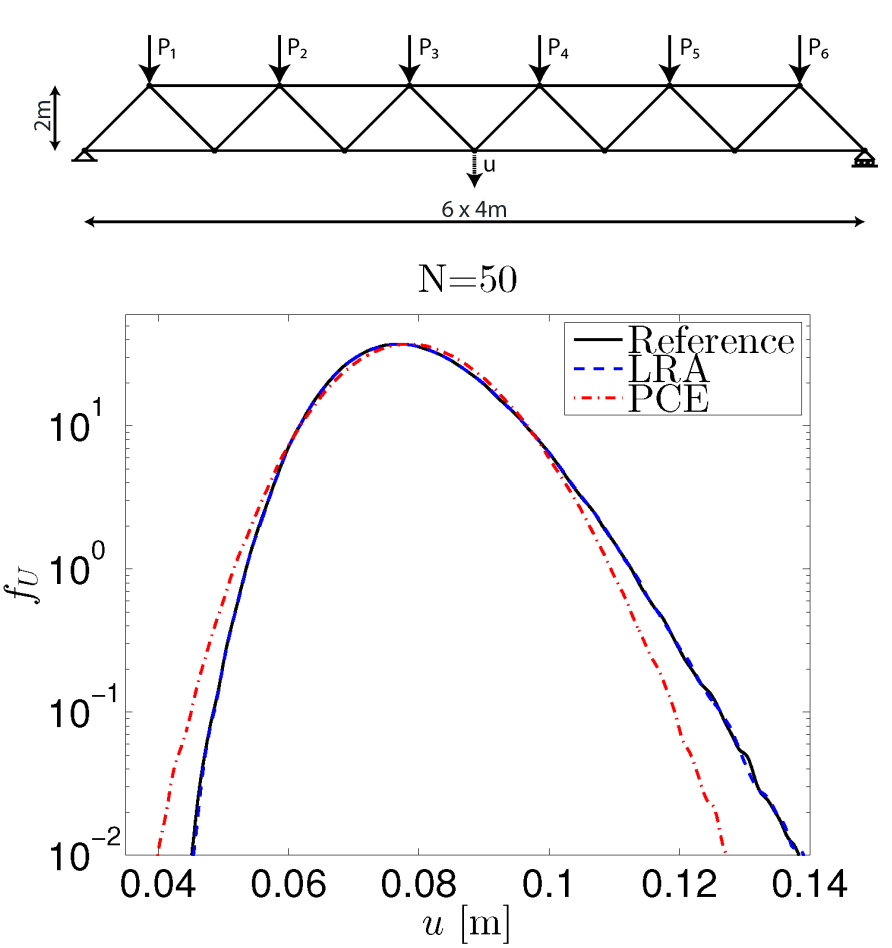
The growing need for uncertainty analysis of complex computational models has led to an expanding use of meta-models across engineering and sciences. Polynomial chaos expansions (PCE) have proven a powerful meta-modeling tool in a wide range of applications, but suffer from the “curse of dimensionality”, namely the exponential increase of the number of unknown coefficients with the input dimension. To address this limitation, the sparse PCE technique was proposed (Blatman and Sudret, 2011). A promising alternative for developing meta-models with polynomial bases in high-dimensional problems is offered by canonical low-rank approximations (LRA). By exploiting the tensor-product form of the polynomial bases, canonical LRA exhibit an only-linear increase of the number of unknown coefficients with the input dimension.
In this project, we investigate the use of canonical LRA with polynomial bases for uncertainty propagation in applications involving finite-element models. We build canonical LRA with a greedy approach, where the rank of the approximation is progressively increased and the polynomial coefficients are computed by means of alternated least-squares minimizations (Chevreuil et al., 2015). We demonstrate that the resulting meta-models provide highly accurate representations of the probability density function (PDF) of the response at the tails and are thus appropriate for the estimation of rare-event probabilities in reliability analysis (Konakli and Sudret, 2015). Furthermore, we employ canonical LRA for sensitivity analysis by means of variance decomposition; to this end, we derive analytical expressions for the Sobol’ indices by post-processing the meta-model coefficients. Canonical LRA are found to outperform sparse PCE when the available experimental designs are small with respect to the input dimension, a situation that is often encountered in real-life uncertainty-propagation problems.
References
M. Chevreuil, R. Lebrun, A. Nouy, P. Rai, A least-squares method for sparse low rank approximation of multivariate functions, SIAM/ASA J. Uncertainty Quantification 3 (1) (2015) 897-921.
G. Blatman, B. Sudret, Adaptive sparse polynomial chaos expansion based on least angle regression, J. Comput. Phys. 230 (2011) 2345-2367.