Surrogate-based reliability analysis for non-deterministic models (GREYDIENT)

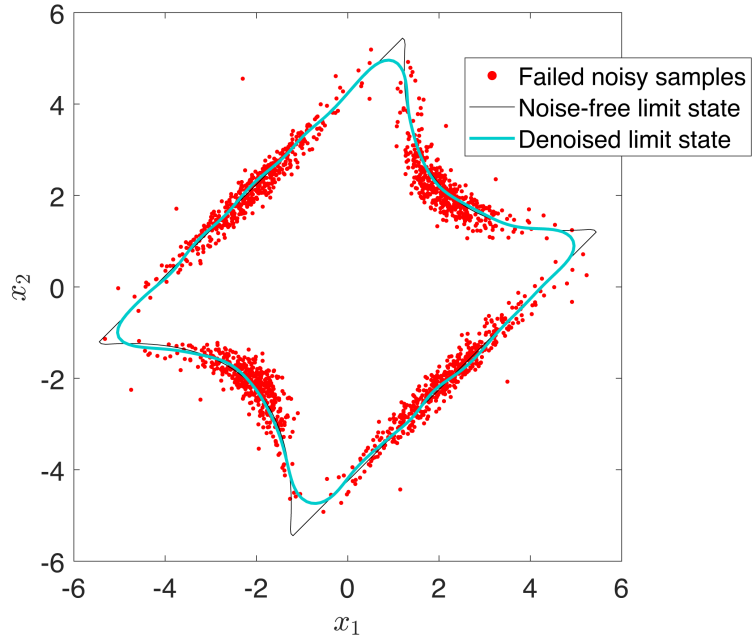
Reliability analysis provides a quantitative approach to assessing the effects of uncertainties on the performance of a system. Its final goal is to compute the probability of failure of the system, which usually requires many evaluations of a limit state function. The latter indicates whether the system fails or not and often relies on expensive computational models. Historically, reliability analysis only deals with deterministic limit state functions. However, engineering models are frequently contaminated by some form of noise, which causes them to behave non-deterministically. Two broad classes of non-deterministic models can be identified: noisy (Pires et al., 2022) and stochastic (Hao et al., 2021). Noisy models present a reducible form of noise related to computational or experimental setups. On the other hand, stochastic models contain irreducible noise caused by latent variability that is not explicitly modelled.

As part of the EU GREYDIENT ITN, this project aims at extending the state-of-the-art in reliability analysis to non-deterministic limit state functions. In the first stage of the project, we show that the denoising of the limit state function is needed to estimate the reliability of noisy models. To achieve this goal, we propose the use of regression-based surrogate models in conjunction with active learning. We demonstrate that they can successfully denoise the problem, and alleviate the computational cost associated with the expensive limit state function, leading to the accurate and efficient estimation of the probability of failure.

More about the GREYDIENT network can be found external page here!

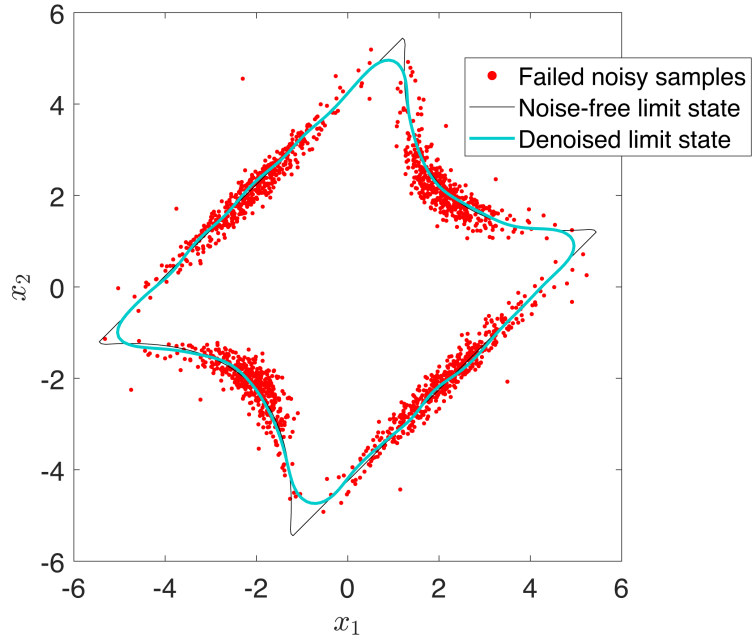
Die Zuverlässigkeitsanalyse bietet einen quantitativen Ansatz zur Untersuchung der Auswirkungen von Unsicherheiten auf die Leistung eines Systems. Ihr Endziel ist die Berechnung der Ausfallwahrscheinlichkeit des Systems, was in der Regel viele Auswertungen einer Grenzzustandsfunktion erfordert. Letztere gibt an, ob das System ausfällt oder nicht, und stützt sich häufig auf teure Rechenmodelle. In der Vergangenheit hat sich die Zuverlässigkeitsanalyse nur mit deterministischen Grenzzustandsfunktionen befasst. Technische Modelle sind jedoch häufig von irgendeiner Form von Rauschen betroffen, was dazu führt, dass sie sich nicht-deterministisch verhalten. Es lassen sich zwei grosse Klassen von nicht-deterministischen Modellen unterscheiden: verrauschte (Pires et al., 2022) und stochastische (Hao et al., 2021). Verrauschte Modelle weisen eine reduzierbare Form des Rauschens auf, die mit den Berechnungs- oder Versuchsaufbauten zusammenhängt. Stochastische Modelle enthalten irreduzible Unsicherheit, das durch latente Variabilität verursacht wird, die nicht explizit modelliert wird.

Als Teil des EU GREYDIENT ITN zielt dieses Projekt darauf ab, den aktuellen Stand der Technik in der Zuverlässigkeitsanalyse auf nicht-deterministische Grenzzustandsfunktionen zu erweitern. In der ersten Phase des Projekts zeigen wir, dass das Entrauschen der Grenzzustandsfunktion erforderlich ist, um die Zuverlässigkeit verrauschter Modelle zu schätzen. Um dieses Ziel zu erreichen, schlagen wir die Verwendung von regressionsbasierten Ersatzmodellen in Verbindung mit aktivem Lernen vor. Wir zeigen, dass sie das Problem erfolgreich entrauschen und die mit der teuren Grenzzustandsfunktion verbundenen Rechenkosten verringern können, was zu einer genauen und effizienten Schätzung der Ausfallwahrscheinlichkeit führt.