Spectral, trajectory-based surrogate models for stochastic simulators

Uncertainty propagation aims at characterizing the influence of input uncertainties on the output of a (computer) model. Traditionally, the uncertainties in all the relevant input variables are explicitly modelled in a probabilistic framework before the uncertainty is propagated through the model. However, in some cases not all the uncertain inputs can or should be quantified, causing the model to feature intrinsic stochasticity. Such a model is called a stochastic simulator: even when all model parameters are held fixed, the output of the model is still a random variable.

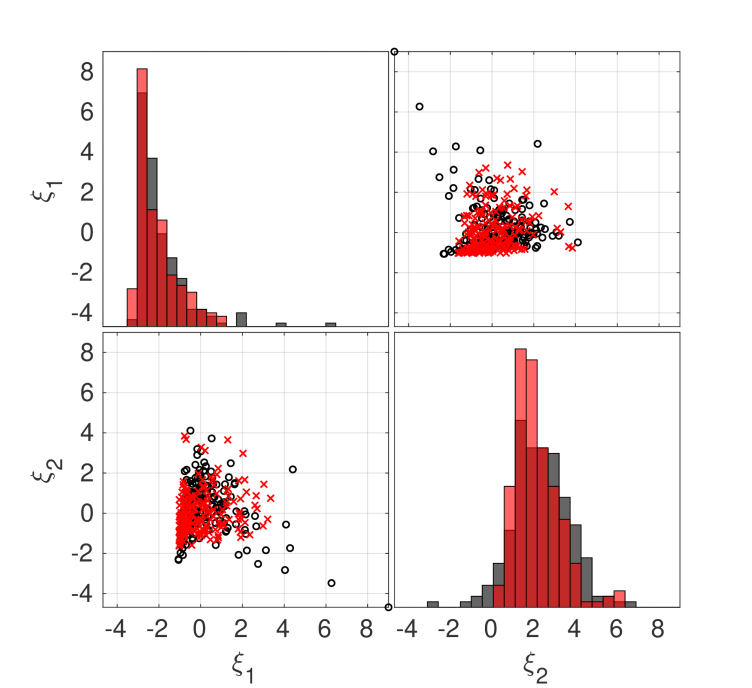
In this project, we develop a new surrogate model for stochastic simulators by viewing the simulator as a (non-Gaussian, non-stationary) random field for which the space of input parameters acts as the index set (external page Lüthen et al., 2023). We approximate its trajectories by sparse polynomial chaos expansions and perform Karhunen–Loève expansion on them. The joint distribution of the random coefficients (see the figure on the left) is inferred using the marginal-copula framework (external page Torre et al., 2019). The resulting surrogate model is able to approximate marginal distributions, mean, and covariance function of the stochastic simulator, and can generate new trajectories.

Die Unsicherheitsfortpflanzung zielt darauf ab, den Einfluss von Eingabeunsicherheiten auf die Ausgabe eines (Computer-)Modells zu untersuchen. Traditionell werden die Unsicherheiten in allen relevanten Eingabevariablen explizit probabilistisch modelliert, bevor die Unsicherheit durch das Modell geleitet wird. In einigen Fällen können oder sollen jedoch nicht alle unsicheren Eingaben quantifiziert werden, so dass das Modell eine inhärente Stochastizität aufweist. Ein solches Modell wird als stochastischer Simulator bezeichnet: Selbst wenn alle Modellparameter fixiert sind, ist die Ausgabe des Modells immer noch eine Zufallsvariable.

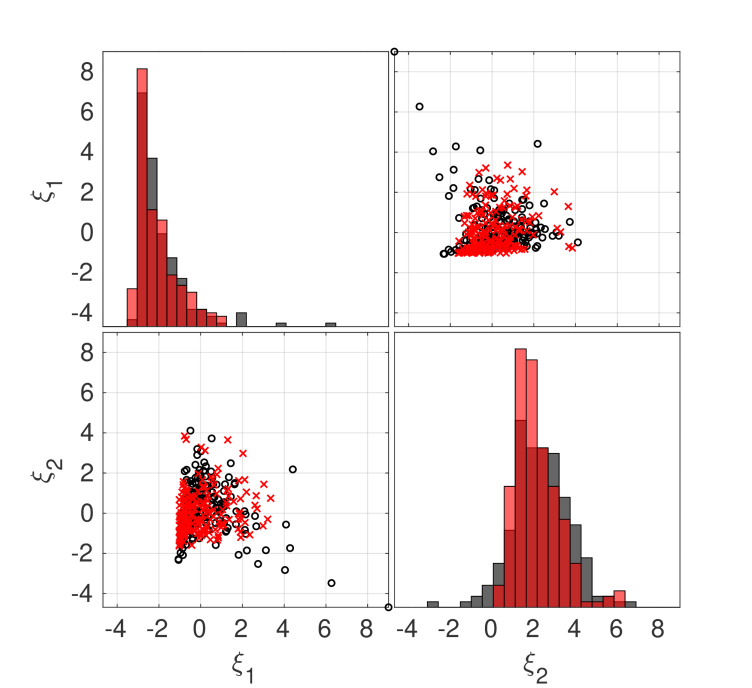
In diesem Projekt entwickeln wir ein neues Ersatzmodell für stochastische Simulatoren, indem wir den Simulator als ein (nicht-Gauss'sches, nicht-stationäres) Zufallsfeld betrachten, für das der Raum der Eingabeparameter als Indexmenge dient (external page Lüthen et al., 2023). Wir approximieren seine Trajektorien mithilfe von dünnbesetzten Polynomial Chaos Expansions und führen eine Karhunen-Loève-Expansion auf ihnen durch. Die gemeinsame Verteilung der Zufallskoeffizienten (siehe Abbildung) wird mit Hilfe der Marginal-Copula-Methode ermittelt (external page Torre et al., 2019). Das daraus resultierende Ersatzmodell ist in der Lage, die Marginalverteilungen, den Mittelwert und die Kovarianzfunktion des stochastischen Simulators zu approximieren und neue Trajektorien zu erzeugen.