Data-driven machine learning regression using polynomial chaos expansions

Machine learning (ML) regression aims to make data-based predictions of system responses to a set of inputs. Popular tools such as artificial neural networks (ANNs) typically work sub-optimally on small data sets, involve significant parameter tuning, and do not explicitly account for uncertainty in the inputs. To counter these shortcomings, we investigate the performance of polynomial chaos expansions (PCE) as a tool for data-driven machine-learning regression.

PCE is a well-established spectral technique in uncertainty quantification, where it is used to replace a computationally expensive model subject to uncertain inputs with a polynomial metamodel. The latter enables an accurate and inexpensive evaluation of the statistics of the system response to the random inputs.

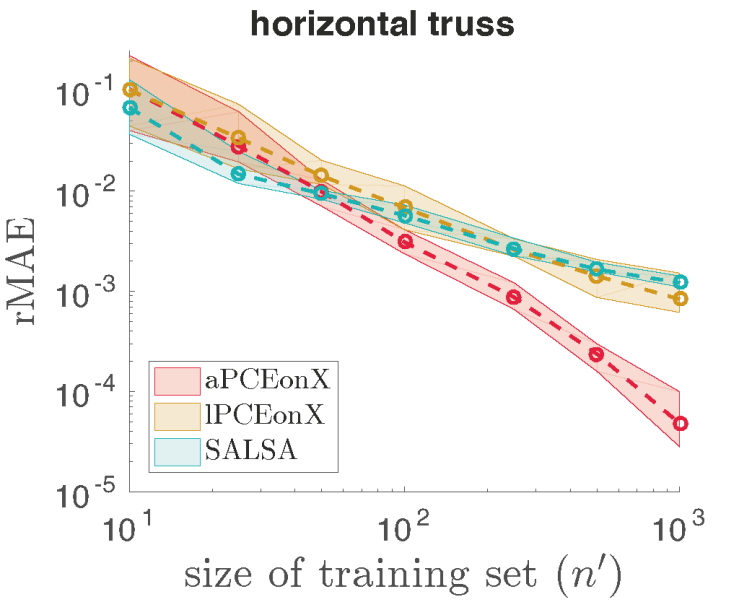
In data driven settings, however, neither the model of the system nor the joint distribution of the inputs are available, but must be determined directly from the data. We demonstrate that constructing a PCE model through sparse regression directly from data yields accurate and robust metamodels, even in the presence of high amplitude noise. Of particular interest are problems where the size of the training data is relatively small compared to the number of inputs, a difficult scenario for many established machine learning techniques.

Im Feld des maschinellen Lernens zielt Regression darauf ab, datenbasierte Vorhersagen von Antworten des Systems auf eine Reihe von Eingaben zu erstellen. Beliebte Methoden wie künstliche neuronale Netze (ANNs) bleiben mit kleinen Datensätzen oft hinter den Erwartungen zurück, erfordern langwierige genaue Abstimmung ihrer Parameter und berücksichtigen die Eingabeungewissheiten nicht. Um diesen Unzulänglichkeiten zu begegnen, untersuchen wir die Anwendbarkeit von polynomial chaos expansions (PCE) auf datenbasierte Regression im Kontext von maschinellem Lernen.

In der Ungewissheitsquantifizierung sind PCE eine etablierte spektrale Methode zum Ersetzen eines rechenintensiven Modells mit ungewissen Eingaben durch ein polynomielles Metamodel. Letzteres erlaubt die genaue und kostengünstige Auswertung von Statistiken der Systemantwort aufgrund ungewisser Eingaben.

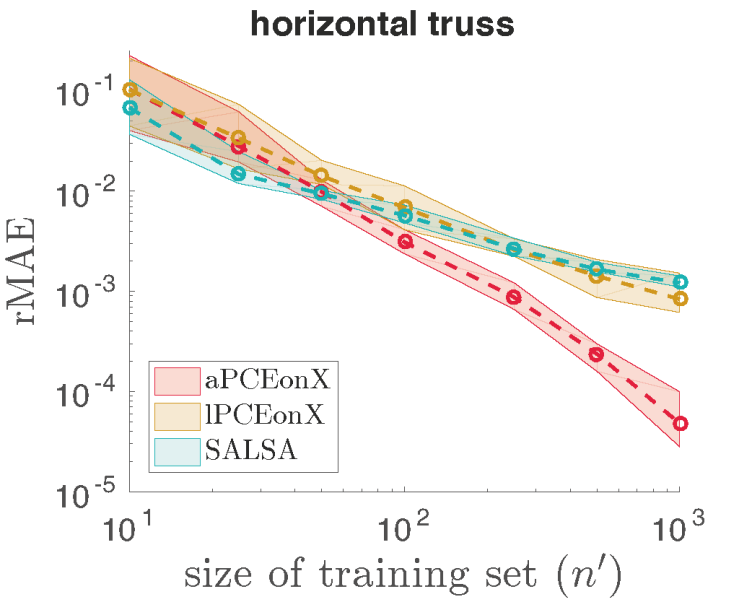
In datenbasierten Szenarien sind allerdings weder ein Modell für das System noch die Verteilung der Eingabeparameter verfügbar. Sie müssen direkt aus den Daten ermittelt werden. Wir zeigen, dass ein PCE-Modell mittels dünnbesetzter Regression direkt aus den Daten erstellt werden kann und genaue und robuste Metamodelle liefert, sogar in der Gegenwart von Rauschen. Besonders interessant sind dabei Probleme, bei denen die Grösse des Datensatzes im Vergleich zur Zahl der Eingabeparameter relativ gering ist, da dies für etablierte Techniken des maschinellen Lernens eine grosse Schwierigkeit darstellt.