Surrogate modeling with discrete and categorical input variables

In modern engineering, it is necessary to consider and quantify uncertainties in a complex system to meet the growing demand of its performance. To this end, simulators are typically required to be evaluated many times. This, however, becomes impracticable for high-fidelity models due to the expensive computational cost. To alleviate the burden, surrogate models can be constructed to emulate the original model.

Classical surrogate models, e.g., polynomial chaos expansions (PCE), are usually designed to tackle problems with the uncertain parameters being continuous. However, many problems in engineering and applied science nowadays involve discrete and categorical variables, for which the development of suitable surrogate models remains less mature.

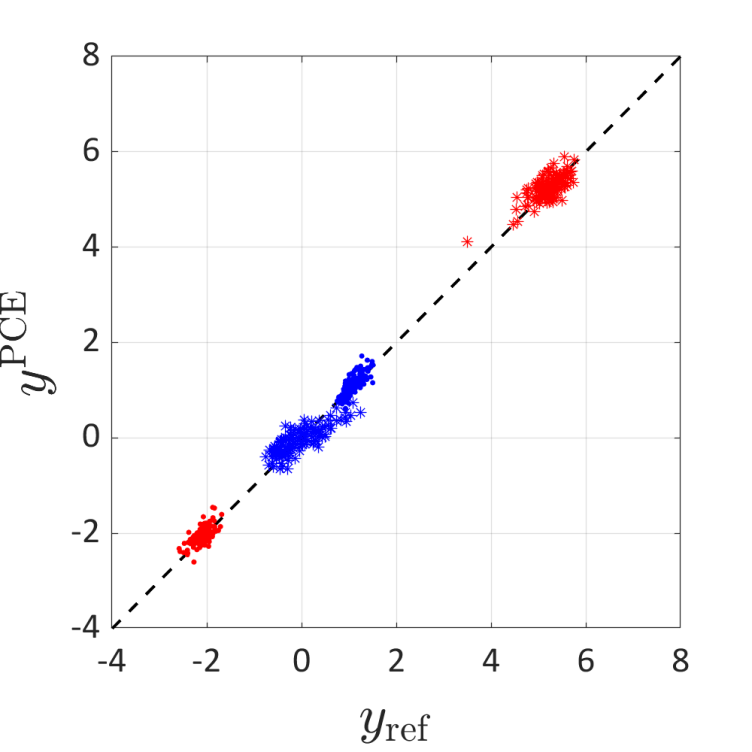
In this project, we extend PCE to solving problems with discrete or categorical variables. For discrete variables, we treat them in the same way as continuous random variables, but the number of the associated polynomial basis functions can be finite (depending on the support of the random variable). For categorical variables, we encode them by quantitative dummy variables, which allows for expressing the problem in the standard regression manner. In addition, we plug this model into the polynomial-chaos-Kriging framework to further improve its accuracy.