Bayesian calibration using stochastic spectral embedding
Principal investigator: P.-R. Wagner
Description
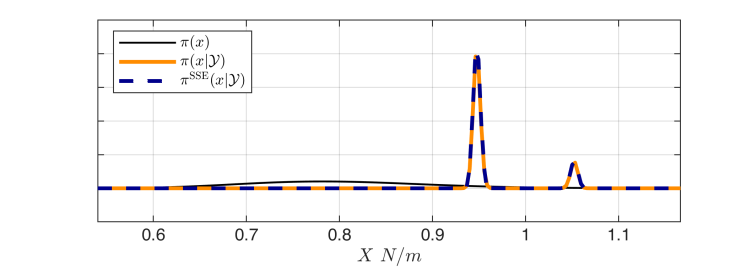
Inverse problems are ubiquitous in engineering and the applied sciences. The calibration of computational models is a particularly important class of inverse problems. The Bayesian framework for model inversion is the most versatile and general approach for probabilistic model calibration. The idea of this framework is to update a prior distribution of the model parameters using a likelihood function containing measurements of the model output to a posterior distribution.
There exists various methods to solve this problem in practice (Markov chain Monte Carlo, Laplace approximation, transport maps, etc.). Another approach called spectral likelihood expansions (SLE) external page [1] solves the problem by expanding the likelihood function onto an orthogonal basis using techniques of sparse polynomial chaos expansions (PCE). Due to the orthogonality of the basis, this approach allows the analytical computation of many posterior statistics. However, the approach is not practical in situations where the data is very informative, resulting in an extremely peaked likelihood.
In this project, we aim to solve this problem by replacing PCE by stochastic spectral embedding (SSE) external page [2] and extend it with an adaptive sample enrichment scheme. This approach maintains the analytical post-processing capabilities of SLE and outperforms it in the case of peaked posteriors external page [3].
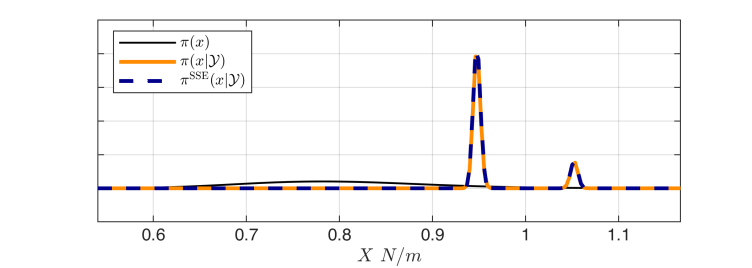
Inverse Probleme sind im Ingenieurwesen und in den angewandten Wissenschaften allgegenwärtig. Die Kalibrierung von Rechenmodellen ist eine besonders wichtige Klasse inverser Probleme. Der vielseitigste und allgemeinste Ansatz dafür ist die Bayes'sche Kalibrierung. Die Idee dieses Verfahrens besteht darin, eine a-priori Verteilung der Modellparameter unter Verwendung einer auf Messungen basierenden Likelihood-Funktion zu einer a-posteriori Verteilung zu aktualisieren.
Es gibt verschiedene Methoden, um dieses Problem in der Praxis zu lösen (Markov-chain Monte Carlo, Laplace-approximation, transport maps, usw.). Ein anderer Ansatz, der als spectral likelihood expansions (SLE) external page [1] bezeichnet wird, löst das Problem, indem die Likelihood-Funktion unter Verwendung von Techniken der dünnbesetzten polynomial chaos expansions (PCE) auf eine orthogonale Basis expandiert wird. Aufgrund der Orthogonalität der Basis ermöglicht dieser Ansatz die analytische Berechnung vieler a-posteriori Statistiken. Der Ansatz ist jedoch in Situationen nicht praktikabel, in denen die Daten sehr informativ sind, was zu einer stark konzentrierten Likelihood-Funktion führt.
In diesem Projekt möchten wir dieses Problem lösen, indem wir PCE durch stochastische spektrale Einbettung (SSE) ersetzen external page [2] und diese mit einer adaptiven Stichprobenanreicherung erweitern. Dieser Ansatz behält die analytischen Nachbearbeitungsfähigkeiten von SLE bei und ist ihr bei stark konzentrierten a-posteriori Verteilungen überlegen external page [3].