Dimensionality reduction and surrogate modelling for Bayesian tomographic imaging

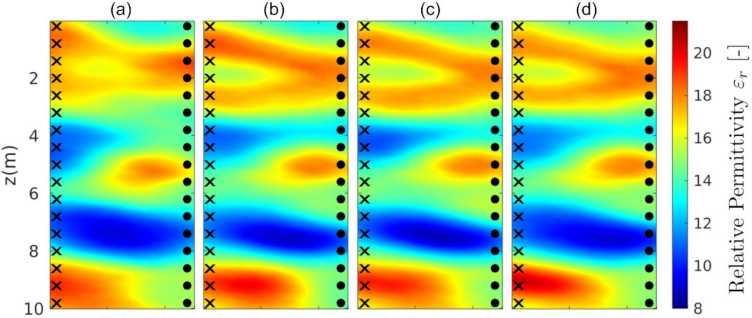
Geophysical tomographic imaging is a highly developed field of research that couples Bayesian inversion with high-accuracy computational models, to provide detailed images of the subsurface. Despite being well-established in many research fields, from hydrology to near-surface oil and gas exploration and monitoring, its computational costs often require access to large high-performance-computing facilities. As result, they are either handled with simplified modelling strategies (e.g. eikonal approximation for travel-time tomography), or with gradient-based, maximum-likelihood estimators that cannot provide confidence bounds on the final reconstructed images, or even converge properly. Moreover, the resolution of tomographic images is generally relatively high, requiring the inversion of thousands- to hundreds of thousands of parameters at a time, a problem typically dealt with by adding heavy regularization constraints to the likelihood function.

Within a collaboration with the Institute of Geophysics at the University of Lausanne, we introduced a novel approach to represent prior information on a lower dimensional stochastic manifold. It is fully data-driven, and only relies on a limited dataset of realizations of some unknown generative prior model. This has the further advantage to completely detach forward and inverse model parameterizations, and does not require ad-hoc regularization in the likelihood (Meles et al., 2022). Additionally, we adopt state-of-the-art surrogate modelling techniques on the reduced-dimensionality manifold to reduce the overall computational burden, without resorting to simplified physics models. We demonstrate that we can achieve comparable fully stochastic tomographic images at a fraction of the original computational costs, without significant loss of accuracy.

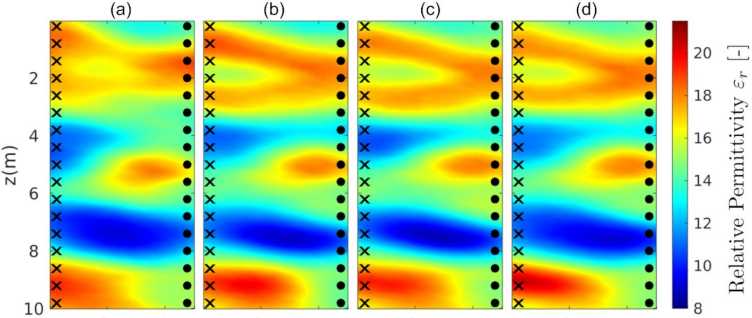
Die geophysikalische tomografische Bildgebung ist ein hochentwickeltes Forschungsgebiet, das die Bayes'sche Inversion mit hochpräzisen Berechnungsmodellen kombiniert, um detaillierte Bilder des Untergrunds zu erstellen. Obwohl sie in vielen Forschungsbereichen - von der Hydrologie bis hin zur oberflächennahen Öl- und Gasexploration und -überwachung - gut etabliert sind, erfordern ihre Berechnungskosten häufig den Zugang zu grossen, leistungsstarken Rechenanlagen. Daher werden sie entweder mit vereinfachten Modellierungsstrategien (z.B. eikonale Annäherung für die Laufzeittomographie) oder mit gradientenbasierten Maximum-Likelihood-Schätzern behandelt, die keine Zuverlässigkeitsgrenzen für die endgültigen rekonstruierten Bilder liefern oder nicht einmal richtig konvergieren. Darüber hinaus ist die Auflösung tomographischer Bilder in der Regel hoch, so dass Tausende bis Hunderttausende von Parametern gleichzeitig invertiert werden müssen, ein Problem, das in der Regel durch Hinzufügen von Regularisierungsbedingungen zur Likelihood-Funktion gelöst wird.

In Zusammenarbeit mit dem Institut für Geophysik der Universität Lausanne haben wir einen neuen Ansatz zur Darstellung von Vorinformationen auf einer niedrigdimensionalen stochastischen Mannigfaltigkeit eingeführt. Dieser Ansatz ist vollständig datengesteuert und stützt sich nur auf einen begrenzten Datensatz von Realisierungen eines unbekannten generativen Anfangsmodells. Dies hat den weiteren Vorteil, dass Vorwärts- und Rückwärtsmodellparametrisierungen vollständig getrennt werden können und keine Ad-hoc-Regularisierung in der Likelihood-Berechnung erforderlich ist (Meles et al., 2022). Darüber hinaus verwenden wir modernste Ersatzmodellierungstechniken in den reduzierten Dimensionen, um die Gesamtberechnungskosten zu senken, ohne auf vereinfachte physikalische Modelle zurückzugreifen. Wir zeigen, dass wir ohne signifikante Einbussen bei der Genauigkeit vergleichbare vollständig stochastische tomografische Bilder zu einem Bruchteil der ursprünglichen Rechenkosten erzielen können.