Optimal experimental designs for adaptive sparse polynomial chaos expansions

In the context of metamodeling, sparse Polynomial Chaos Expansions (PCE) based on least angle regression (LARS) have gained popularity in the recent years because of their ability to model highly non-linear responses with low fitting cost (Blatman & Sudret, 2011). Although sparse PCEs are efficient and versatile, the quality of approximation strongly depends on the choice of the experimental design (ED), i.e. the sample points where the original computational model is evaluated. Moreover, a minimum number of calls to the deterministic model is aimed at. 

In this project, we investigate the selection of the best design of experiments (the size of which is defined by the analyst) in order to ensure the optimal accuracy of the surrogate model over the whole input space. As model evaluations are time-consuming, it is appropriate to build up the ED sequentially by enriching an initial design, based on the information gathered at the previous iteration. The initial ED, which is generated using a space-filling technique, is enriched sequentially using an optimality criterion. This criterion is related to the orthogonality of columns of the information matrix, as proposed by Shin & Xiu (2016). 

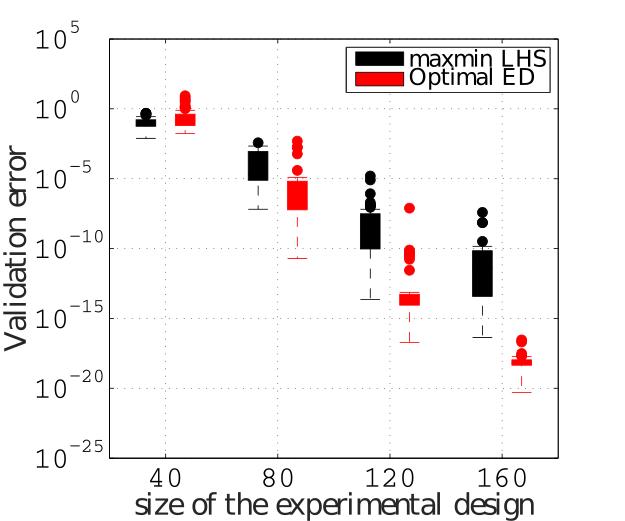
Figure 1 shows the results of a comparative study between the sequential optimal design and a standard maximin LHS, with boxplots presenting the quartiles and median validation error based on 50 independent runs for varying sizes. The figure shows that the proposed optimal design outperforms notably maximin LHS.

References

Blatman, G., and Sudret, B. (2011). Adaptive sparse polynomial chaos expansion based on Least Angle Regression. Journal of Computational Physics, 230(6), 2345-2367.

Shin, Y., and Xiu, D. (2016). Nonadaptive quasi-optimal points selection for least squares linear regression. SIAM Journal on Scientific Computing, 38(1), A385-A411.