Uncertainty quantification and global sensitivity analysis in epidemiological models

Epidemiological models are powerful tools for the understanding and prediction of disease propagation. In some cases, such models are used by policy-makers and legislative bodies to devise prevention and mitigation strategies.

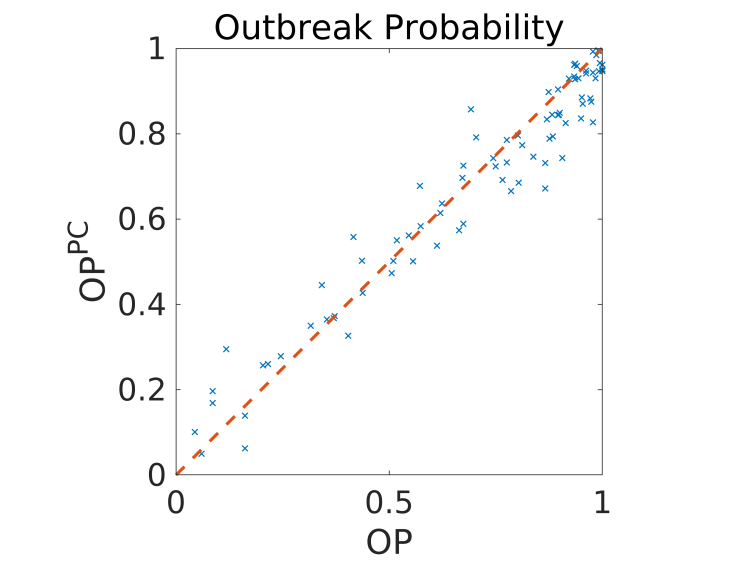
In this project, we tackle the task of introducing uncertainty quantification in the epidemiological modelling community. In particular, we focus on the sensitivity analysis of agent-based rabies propagation models. Agent-based models for disease propagation are particularly challenging in standard uncertainty quantification settings: their response is non-deterministic even for perfectly known boundary conditions (i.e. they are so-called stochastic simulators), and they can be high dimensional. To bypass these challenges, uncertainty quantification is performed on the statistics (moments and quantiles) of repeated model evaluations at a restricted set of input parameter configurations. The convergence of the analysis is ensured by the use of sparse polynomial chaos expansions, which are known to be robust to noise in the estimator of the statistics of the model response [1].

Epidemiologische Modelle sind leistungsfähige Werkzeuge zum Verständnis und zur Vorhersage von Krankheitsausbreitungen. In manchen Fällen werden sie von politischen Entscheidungsträgern und Gesetzgebern verwendet, um Präventions- und Minderungsstrategien zu entwickeln.

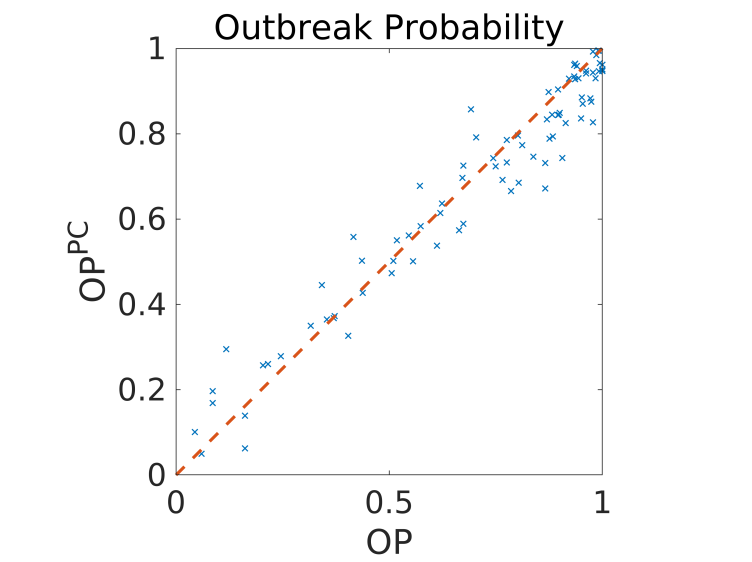
In diesem Projekt stellen wir uns der Aufgabe, die Ungewissheitsquantifizierung in die epidemio-logische Modellierungsgemeinschaft einzuführen. Wir konzentrieren uns insbesondere auf die Sensitivitätsanalyse von agentenbasierten Ausbreitungsmodellen für Tollwut. Agentenbasierte Modelle für die Krankheitsausbreitung stellen eine besondere Herausforderung dar: Ihr Verhalten ist selbst für genau bekannte Randbedingungen nicht deterministisch (d.h. sie sind sogenannte stochastische Simulatoren) und sie können hoch-dimensional sein. Um diese Herausforderungen zu umgehen, wird die Unsicherheitsquantifizierung der Statistiken (Momente und Quantile) wiederholter Modellauswertungen mit einer begrenzten Anzahl von Eingabeparametern durchgeführt. Die Konvergenz der Analyse wird durch die Verwendung von dünnbesetzten polynomial chaos expansions sichergestellt. Diese sind robust gegenüber Störungen im Schätzer von Statistiken der Modellantwort [1].