Efficient representation and propagation of imprecise probability using p boxes

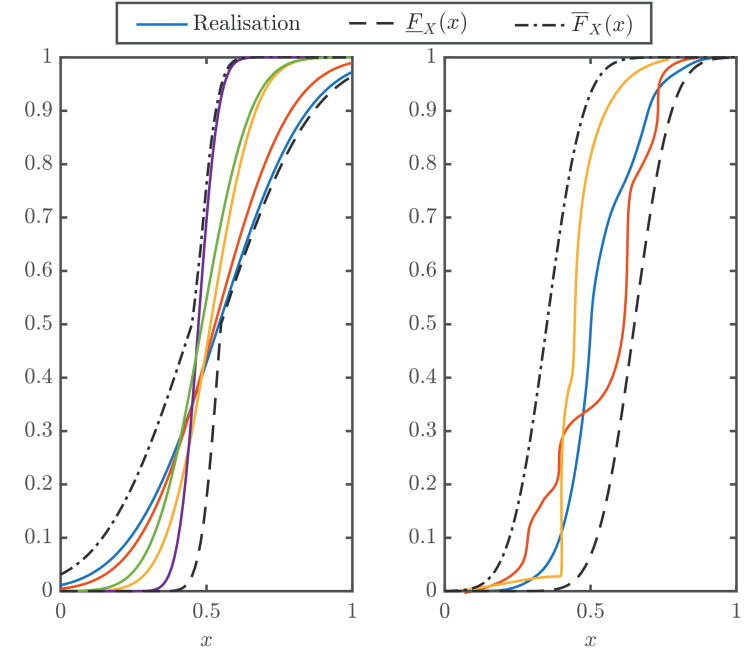
Imprecise probability theory is a key ingredient of uncertainty quantification, when the roles of aleatory and epistemic uncertainty need to be dealt with separately. Among the many available tools to represent and propagate such uncertainties, p-boxes are among the best known. They provide a natural bridge between pure interval analysis and probabilistic methods, by representing uncertainty with upper and lower bounds on the underlying cumulative probability distribution.

In this project we explore how staple tools from the classical “probabilistic” uncertainty quantification arsenal can be incorporated organically into the representation and propagation of uncertainty with p-boxes. These include both a comprehensive review and reformulation of the concepts of imprecise probability, as well as the design and validation of a new family of probability boxes, that takes into account statistical constraints on the underlying distribution properties. A contribution to the review paper [1] was also a part of this project. 

Die sogenannte unpräzise Wahrscheinlich-keitstheorie ist ein wichtiger Bestandteil der Ungewissheitsquantifizierung, wenn aleatorische und epistemische Ungewissheiten getrennt betrachtet werden sollen. Unter den vielen dafür verfügbaren Methoden, die solche Ungewissheiten modellieren und fortpflanzen, sind p-Boxes wohl die bekanntesten. Diese stellen eine natürliche Brücke zwischen reiner Intervallanalyse und wahrscheinlichkeitstheoretischen Methoden dar, indem sie Ungewissheit durch obere und untere Schranken für die zugehörige Verteilungsfunktion repräsentieren.

In diesem Projekt untersuchen wir, wie Standardmethoden aus dem Arsenal der klassischen wahrscheinlichkeitstheoretischen Ungewissheits-quantifizierung organisch für die Darstellung und Fortpflanzung von Ungewissheiten mit p-Boxes verwendet werden können. Wir führen eine umfassende Literaturübersicht durch und formulieren einige Konzepte der unpräzisen Wahrscheinlichkeit um. Ausserdem entwickeln und validieren wir eine neue Familie von p-Boxes, die Nebenbedingungen für die statistischen Eigen-schaften der zugehörigen Verteilung berücksichtigt. Ein weiterer Aspekt des Projekts war unser Beitrag zum Übersichtsartikel [1].