Vine copulas for uncertainty quantification

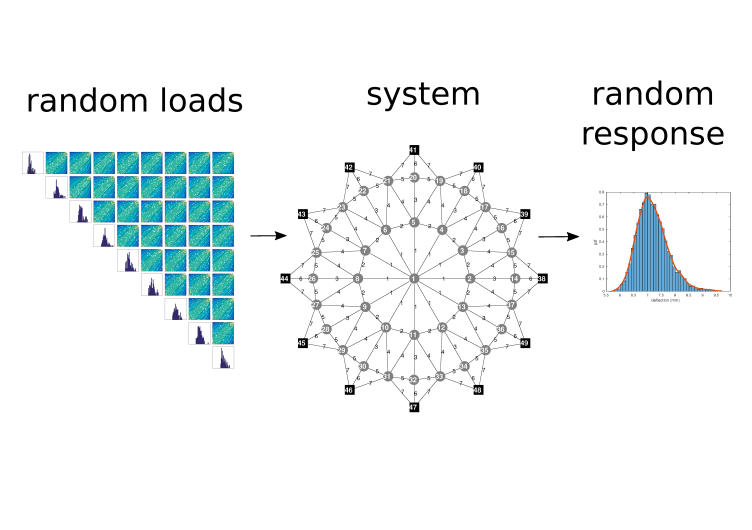
Uncertainty quantification (UQ) aims to draw accurate statistics of the response of systems subject to uncertain (random) inputs. Research on UQ has largely focused on improving algorithms to draw the output statistical estimates, assuming the input distribution (PDF) to be known. The aspect of representing the joint PDF with accurate probabilistic models has received comparably less attention.

With the increase in problem dimensionality and complexity, the need for detailed probabilistic representations of the inputs is becoming a central topic in the field. In this context, the dependence structure between the parameters plays a particularly crucial - and so far underappreciated - role, especially when the estimation of low probability events is considered. Copula theory and inference form a natural framework for representing this dependence.

In this project we develop a suitable set of techniques and software tools that enable the usage of state-of-the art uncertainty quantification algorithms in the presence of complex input dependencies modelled by vine copulas. Associated inference methods ensure applicability to problems where the inputs are only known through data sets of measurements, and their underlying joint distribution is unknown.

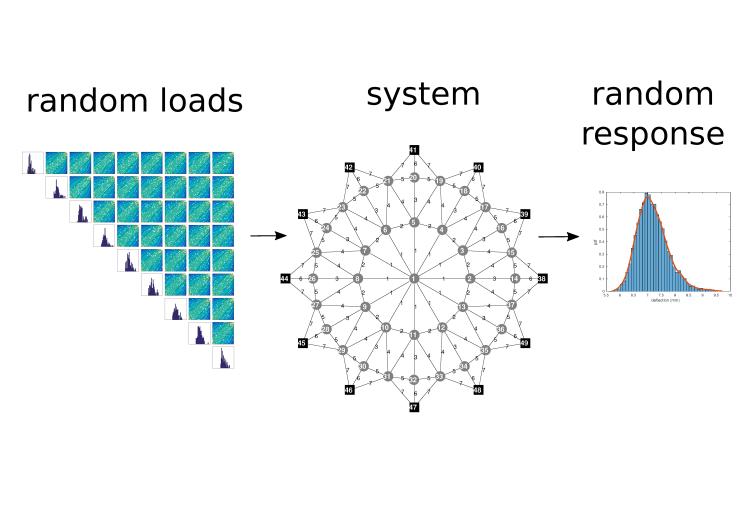
Ungewissheitsquantifizierung (UQ) zielt darauf ab, genaue Statistiken von Systemausgaben unter ungewissen (zufälligen) Eingaben zu berechnen. Forschung im Bereich von UQ hat sich bisher im Wesentlichen darauf konzentriert, unter Annahme bekannter Eingabeverteilungen die Algorithmen zur Berechnung der Ausgabestatistiken zu verbessern. Die genaue probabilistische Modellierung der multivariaten Verteilung von Eingabeparametern hat hingegen vergleichsweise wenig Beachtung gefunden.

Die genaue probabilistische Darstellung der Eingabeparameter ist ein zentrales Thema in UQ, zumal die betrachteten Probleme zunehmend hochdimensional und komplex werden. Die Abhängigkeitsstruktur zwischen Parametern spielt eine wesentliche und bisher vernachlässigte Rolle, besonders wenn Wahrscheinlichkeitsereignisse mit geringer Wahrscheinlichkeit betrachtet werden. Copula-Theorie und Inferenz bilden ein natürliches Framework für die Darstellung dieser Abhängigkeit.

In diesem Projekt entwickeln wir geeignete Techniken und Software, um die Verwendung von hochmodernen UQ-Algorithmen im Falle von komplexen Eingabeabhängigkeiten zu ermöglichen, wobei letztere durch Vine-Copulas modelliert werden. Dazugehörige Inferenzmethoden stellen die Anwendbarkeit auf Probleme sicher, bei denen die Eingaben nur durch Messungen bekannt sind und deren zugrundeliegende multivariate Verteilung unbekannt ist.