Bayesian inversion for the calibration of fire experiments on insulation panels
Description
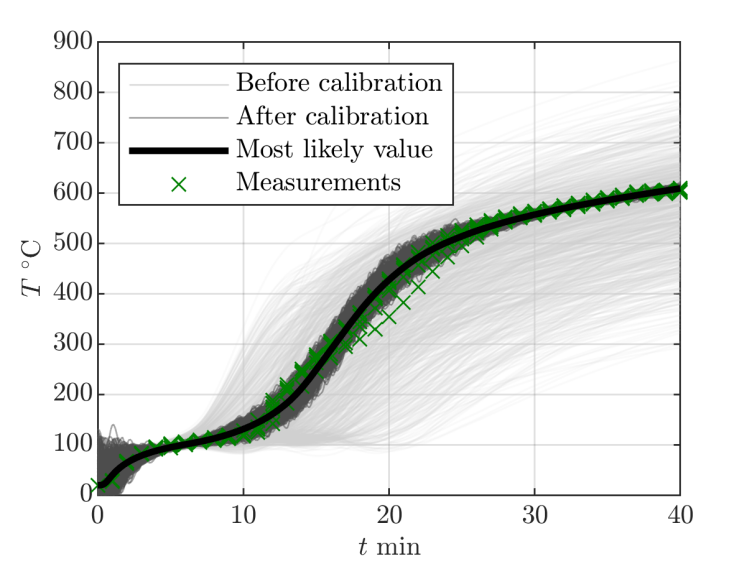
In the setting of structural design for fire hazards the simulation of thermal transport in insulation panels is of great interest. The use of such simulation tools requires the calibration of the underlying heat transport models and their temperature-dependent parameters. The calibration of these quantities is challenging and was in the past attempted with empirical trial-and-error approaches. These approaches are very time consuming, prone to human error, and lack a clear definition of the occurring sources of uncertainty. Due to parameter dependencies, this calibration approach also often yields ambiguous results.
To resolve these problems, the calibration was conducted in a probabilistic setting that allows a clear identification of sources of uncertainties (model error, measurement error, etc.) and returns parameter distributions as opposed to single best-fit values. By applying the well-known Markov chain Monte Carlo (MCMC) based Bayesian inversion approach, the calibration can be carried out in a semi-automatized fashion. To make the procedure computationally feasible, a surrogate model of the nonlinear transient finite element analysis, that combines polynomial chaos expansions and principal component analysis, was employed external page [1].
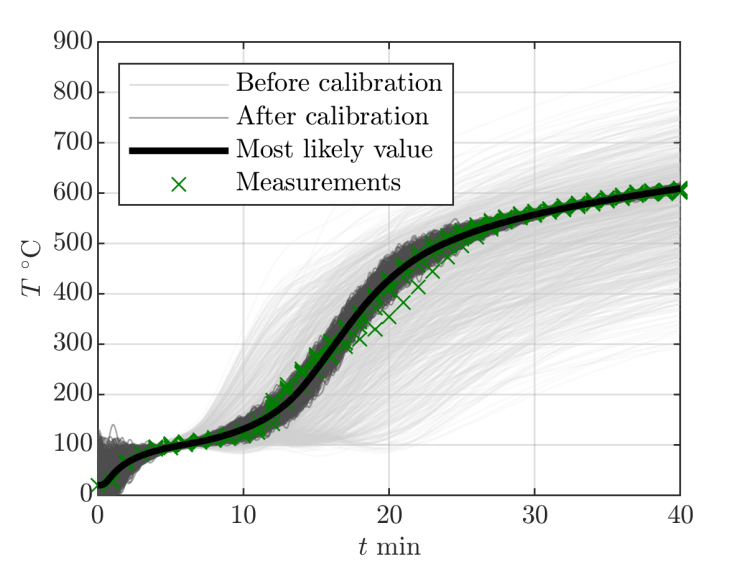
Bei der Tragwerksdimensionierung für Brandgefährdung ist die Simulation des Wärme-transportes in Dämmplatten von großem Interesse. Die Verwendung solcher Simulationswerkzeuge erfordert die Kalibrierung der zugrundeliegenden Modelle und ihrer temperaturabhängigen Parameter. Die Kalibrierung dieser Grössen ist anspruchsvoll und wurde in der Vergangenheit empirisch durchgeführt. Dieser Ansatz ist sehr zeitaufwändig, anfällig für menschliche Fehler und hat keine klare Definition der auftretenden Ungewissheiten. Aufgrund von Abhängigkeits-beziehungen zwischen Parametern führt diese Kalibrierung ausserdem oft zu mehrdeutigen Ergebnissen.
Um diese Probleme zu lösen, wurde die Kalibrierung probabilistisch durchgeführt. Dies ermöglicht die eindeutige Identifizierung von Unsicherheitsquellen (Modellfehler, Messfehler usw.) und liefert Parameterverteilungen statt einzelnen Best-Fit-Werten. Die Kalibrierung erfolgte durch Anwendung der bekannten Bayes’schen Inversion basierend auf Markov-Ketten-Monte-Carlo (MCMC) Sampling. Um das Verfahren rechnerisch zu ermöglichen, wurde ein Ersatzmodell der nichtlinearen transienten Finite-Elemente-Analyse verwendet, welches polynomial chaos expansions und Hauptkomponentenanalyse kombiniert external page [1].