Uncertainty quantification with imprecise probabilities

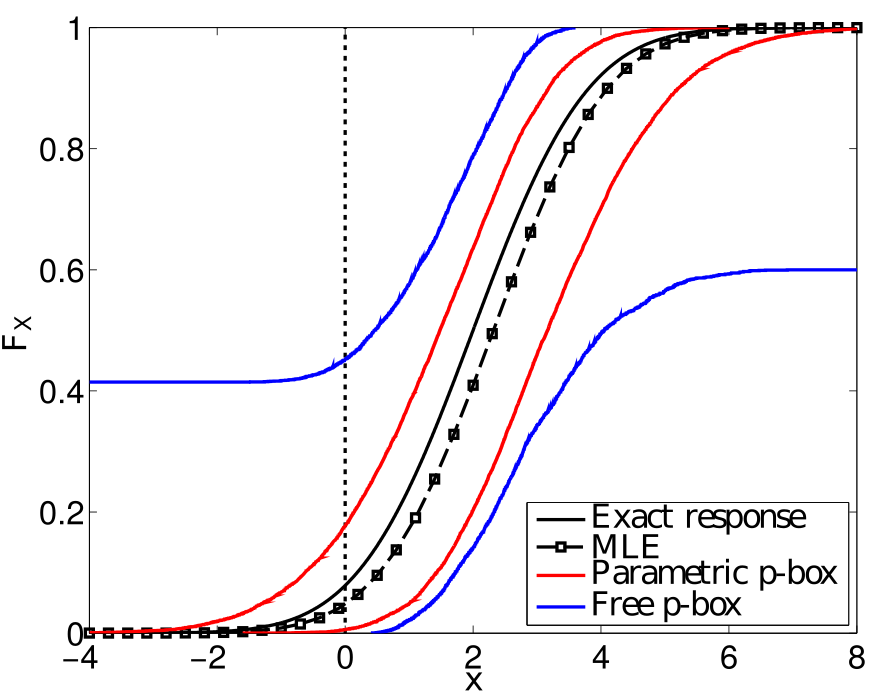
The term “imprecise probabilities” is a vague formulation of many attempts to describe the mix of different sources of uncertainty. The commonly known source is aleatory uncertainty which describes the natural variability of a parameter and is non-reducible. A second source is the so-called epistemic uncertainty, which originates from the lack of knowledge and/or the lack of precision on data. The epistemic uncertainty can be reduced by collecting more pieces of information and/or data.

Both types of uncertainties are inherent in modelling natural processes, which requires the consideration of imprecise probabilities e.g. for reliability analysis. Commonly, only the aleatory uncertainty is considered by using probability theory. However, modelling both sources of uncertainty requires a framework more general than probability theory. Amongst various options (including Dempster-Shafer’s theory of evidence, Bayesian hierarchical modelling, and fuzzy numbers), this project mainly focuses on probability boxes (so-called p-boxes).

With growing computational power and more advanced uncertainty propagation techniques, imprecise probabilities can now be handled in realistic settings. Hence, this project connects the concepts of imprecise probabilities and recent advances in surrogate modelling for propagating p-boxes through complex computational models. New approaches such as polynomial expansions and Kriging will be explored. Finally, the methods are applied to uncertainty propagation, structural reliability analysis and sensitivity analysis.

References